Question

Find an equation of the line passing through the point (3,1) and parallel to the line 3x - Y - 4 =0.

Answer 1

hello

the points given were

`3,1`

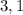
and the equation is parallel to the line

`3x-y-4=0`

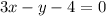
let's rearange this equation

`y=3x-4`

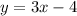
first we find the slope of the line using slope-intercept form

from the equation above, the slope and intercept are

`\begin{gathered} \text{slope(M)=3}_{} \\ \text{ intercept(c)=-4} \end{gathered}`

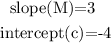
now the equation of the line passing through a point (x1, y1) is given as

`y-y_1=m(x-x_1)`

now the points of the equation are (3, 1)

`\begin{gathered} x_1=3 \\ y_1=1 \\ \text{slope(m)}=3 \end{gathered}`
`\begin{gathered} y-1=3(x-3) \\ y-1=3x-9 \\ y=3x-9+1 \\ y=3x-8 \end{gathered}`

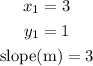
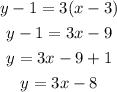
the equation of the line is given as y = 3x - 8