Question

I need help finding out comes

Answer 1

The factorial value 6! indicates the multiplication of all whole numbers from 6 to 1:

`\begin{gathered} 6!=6\cdot5\cdot4\cdot3\cdot2\cdot1 \\ 6!=720 \end{gathered}`

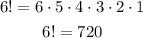
To determine the possible ways two people can be chosen from six, you have to use combinations following the expression:

`(n!)/((n-x)!)`

For a total of n=6, you have to choose x=2 people:

`\begin{gathered} (6!)/((6-2)!)=(6!)/(4!) \\ ((6\cdot5\cdot4\cdot3\cdot2\cdot1))/((4\cdot3\cdot2\cdot1))=6\cdot5=30 \end{gathered}`

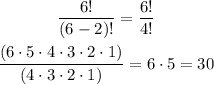
There are 30 possible combinations.

To determine the possible combinations in which you can choose the groups, given that three people can be selected, given that three of the people are asked to sit in front of the other people, which means that these three people can be only be selected once, you have to use the expression:

`\begin{gathered} (6!)/((6-3)!(3)!)=(6!)/(3!\cdot3!) \\ ((6\cdot5\cdot4\cdot3\cdot2\cdot1))/((3\cdot2\cdot1)(3\cdot2\cdot1))=(720)/(36)=20 \end{gathered}`

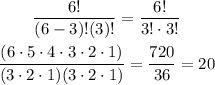
There are 20 possible combinations for the groups, given that three people are sitting in front