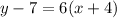The given equation is

The slope of the given line is 6.
It is important to know that parallel lines have the same slopes, so the slope of the new line is 6.
Now, we use the point-slope formula to find the new line

Let's replace the point (-4,7) and the slope 6.

Hence, the equation of the new parallel line in slope-intercept is
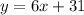
In point-slope form is