Question

Ms, Castillo wants to rebuild her garden. She thinks it needs a modern twist and decides to make a star-shaped garden. The legs of the star will be filled with flowers and the central pentagon will be grass. Here are the dimensions of her stellar garden: each leg of the star is a triangle with two sides, both 20 feet long,and an altinade of 19 feet. The pentagon is regular (the sides are all equal and the angles are all equal), and thedistance from the center of the pentagon to one of the sides is 8.5 feet.Ms. Castillo needs your help to calculate the floral area and grassy area in this new garden design. Then she can figure out the equipment and materials she will need for the project.Square area of the legs of the star:______________Square areas of the center pentagon:_____________

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

leg of the star:

side = 20 ft

height = 19 ft

regular pentagon:

Step 02:

geometry:

area:

area of the legs of the star (triangle):

A = (base * height) / 2

s² = h² + b²

(20 ft)² = (19 ft)² + b²

400 ft² - 361 ft² = b²

39 ft² = b²

`b=\text{ }√(39ft²)=6.25\text{ ft}`

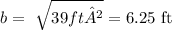
base = 2 * b = 2 * 6.25 ft = 12.50 ft

total area of the legs of the star:

area of the center pentagon:

A = 1/2 a 5 s

The answer is:

total area of the legs of the star = 593.75 ft²

area of the center pentagon = 265.63 ft²