We can find the inverse of f(x) applying:
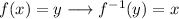
![\begin{gathered} f(x)=\sqrt[3]{x}+7=y \\ \sqrt[3]{x}+7=y \\ \sqrt[3]{x}=y-7 \\ x=(y-7)^3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4w45h5b5ba7cr58qcncs3wwt5dw6qe7seq.png)
The inverse function is:
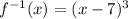
The domain of the inverse function is equal to the range of the original function.
As the range of the original function in this case is "all y", the domain of the inverse function is "all x".