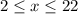Answer:
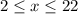
Step-by-step explanation:
Here, we want to get the range of values for the width of the rectangle
We start by representing the width by a variable x
Mathematically, we have the perimeter of the rectangle as:

where l is the length and w is the width of the rectangle
The perimeter in terms of the actual values is thus:
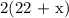
This value is at least 48 ft:
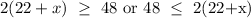
The perimeter is no longer than 88 ft
We have that as:

We have the compound inequality as:
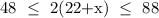
We then proceed to solve the compound inequality as follows:
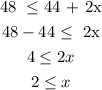
Secondly:
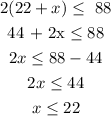
Thus, we have the solution as: