Question

13. Let Enter the angle measure (), in degrees, for sin (60) = 2 13 cos (O)=2

Answer 1

To find the unknown angle, we will have to construct a right triangle which shows the sine of angle 60 degrees, as follows:

Since:

`\sin \text{ }\theta=(opposite)/(hypothenus)`

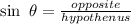
Thus :

`\sin 60^o\text{ = }(opposite)/(hypothenus)=\text{ }\frac{\sqrt[]{3}}{2}`

Now we will have to make a sketch of a right triangle accordingly:

From the sketched diagram, we can see how the sine of angle 60 degrees can be represented on a right triangle.

We can complete the angles in the right traingle, as follows:

Since we have a right angle, and an angle 60 degrees, which altogether sum up to :90 + 60 = 150 degrees, we know that the other angle inside the right triangle has to be 30 degrees since the total angle inside a triangle has to be 180 degrees. This was why we have included it as the

Now:

From the diagram:

`\begin{gathered} \text{From the diagram we can s}ee\text{ that, if we consider the angle 30}^o,\text{ then} \\ \cos 30^{o\text{ }}=(adjacent)/(hypothenus)\text{ = }\frac{\sqrt[]{3}}{2} \\ \text{therefore, the angle }\theta=30^o \end{gathered}`