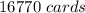Given that there are a total of 130 people at the meeting and each gives a Valentine's Day card to everyone else, you need to use the Permutation Formula in order to calculate the number of cards that were given:
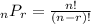
Where "n" is the total number of objects in the set, and "r" is the number of objects selected from the set.
In this case, you can identify that:
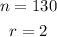
(Notice that the value of "r" is 2 because they give a card to each other).
Then, substituting values into the formula and evaluating, you get:
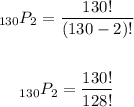
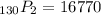
Hence, the answer is: