Answer:
1125
Step-by-step explanation:
To evaluate the expression, we need to substitute x by 5 and y by 4, so we get:
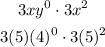
By properties of the exponents, any number to the power of 0 is equal to 1, and any number to the power of 2 is equal to that number multiplied by itself, so:
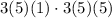
Now, we can multiply the terms of the expression to get:
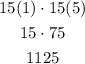
Therefore, the answer is 1125