Question

consider that triangle ABC is an equilateral triangle, and segment AD is a perpendicular bisector of triangle ABC. If AB equals 2x, complete the statements below.

Answer 1

Since AD is a perpendicular bisector to the triangle, that means it divides the base line of the triangle into two 90° angles, as shown in the following image:

And since the two triangles have a 90° angle, they are right triangles. That means that we can use The Pythagorean Theorem in them.

First, we consider that side AB is 2x:

And for the left triangle, the Pythagorean theorem is as follows:

`(BD)^2+(AD)^2=(2x)^2`

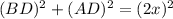
We can represent the Pythagorean theorem also considering that the triangle is equilateral, so all of the sides are equal.

Thus, the side of the base is also 2x, which is divided by AD on two sides of length x, we can see this in the following image:

Since BD is equal to x, we substitute this in the previous formula for the Pythagorean theorem:

`\begin{gathered} (BD)^2+(AD)^2=(2x)^2 \\ x^2+(AD)^2=(2x)^2 \end{gathered}`

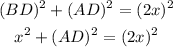
So, for the first blank spare we will have an x.

We continue solving this for AD^2 to find the next blank space.

Subtracting x^2 to both sides:

`(AD)^2=(2x)^2-x^2`

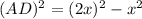
But we need to solve the term 2x to the power of 2:

`(2x)^2=4x^2`

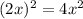
And we substitute this value:

`(AD)^2=4x^2^{}-x^2`

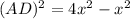
Thus, the second blank space is 4.

To find the next blank space we just need to combine the like terms in the right side, since 4-1 is 3 we get:

`(AD)^2=3x^2`

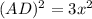
And we find that the third blank space is 3.

Finally, to find the last blank space we need to solve this last equation for AD, and we do that by taking the square root of both sides of the equation:

`\sqrt[]{(AD)^2}=\sqrt[]{3x^2}`

A square root and a power of 2 cancel each other on the left and right sides.

Note: on the right side the 3 will still be inside the square root.

`AD=x\sqrt[]{3}`

And we find that the fourth blank space is x.