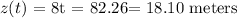Question

Note: Enter your answer and show all the steps that you use to solve this problem in the space provided.Lukalu is rappelling off a cliff. The parametric equations that describe her horizontal and vertical positionas a function of time are z(t) = 8t and y(t) = -16t² + 100 and. How long does it take her toreach the ground? How far away from the cliff is she when she lands?Remember to show all of the steps that you use to solve the problem.

Answer 1

`\begin{gathered} a)\text{ 2.26 seconds} \\ b)\text{ 18.10 meters} \end{gathered}`

Step-by-step explanation:

a) To get the time taken to reach the ground, we set the horizontal and vertical positions equal to one another

Mathematically, we have that as:

`\begin{gathered} z(t)\text{ = y\lparen t\rparen } \\ 8t\text{ = -16t}^2+100 \\ 16t^2+8t-100\text{ = 0} \\ 4(4t^2+2t-25)\text{ = 0} \\ 4t^2+2t-25\text{ = 0} \end{gathered}`

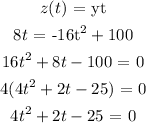
We can proceed to solve for t by using the quadratic equation

We have that as:

`t\text{ = }(-b\pm√(b^2-4ac))/(2a)`

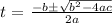
a is the coefficient of t^2 which is 4 , b is the coefficient of t which is 2, c is the last number which is -25

Substituting the values, we have it that:

`\begin{gathered} t\text{ = }(-2\pm√(2^2-4(4)(-25)))/(2(4))\text{ = }(-2\pm√(4+400))/(8) \\ \\ t\text{ = }(-2\pm√(404))/(8) \\ \\ t\text{ = -2.76 or 2.26} \end{gathered}`

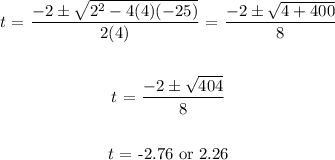
Since t cannot be negative, we have the time as 2.26 seconds

b) To get her distance from the cliff, we find the value of z(t)

We simply substitute t into the equation for z(t)

We have that as:

`\begin{gathered} \\ z(t)\text{ = 8t = 8\lparen2.26\rparen = 18.10 meters} \end{gathered}`