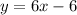1 Answer

Matthieu Moy · Answer 1 · 2023-11-15T17:49:42+0000

First, let's calculate the slope of the line:

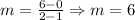
$m=(6-0)/(2-1)\Rightarrow m=6$

Let's use a generic slope-intercept equation, the slope we just calculated and point (1, 0) as following:

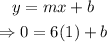
$\begin{gathered} y=mx+b \\ \Rightarrow0=6(1)+b \end{gathered}$

Solving for b (the y-intercept):

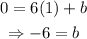
$\begin{gathered} 0=6(1)+b \\ \Rightarrow-6=b \end{gathered}$

This way, we can conclude that the equation of the line in the slope-intercept form is:

Please log in or register to add a comment.