Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. At a candy store, Diana bought 5 pounds of jelly beans and 3 pounds of gummy worms for $58. Meanwhile, Monica bought 6 pounds of jelly beans and 3 pounds of gummy worms for $66. How much does the candy cost? A pound of jelly beans costs $ and a pound of gummy worms costs $ Submit

Answer 1

Let x be the cost of 1 pound of jelly beans

Let y be the cost of 1 pound of gummy worms

Diana bought 5 pounds of jelly beans and 3 pounds of gummy worms for $58:

`5x+3y=58`

Monica bought 6 pounds of jelly beans and 3 pounds of gummy worms for $66:

`6x+3y=66`

System of equations:

`\begin{gathered} 5x+3y=58 \\ 6x+3y=66 \end{gathered}`

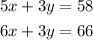
Solve by elimination method:

1. Subtract the equations:

2. Solve x:

`\begin{gathered} -x=-8 \\ x=8 \end{gathered}`

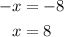
3. Use the value of x to find y:

`\begin{gathered} 5x+3y=58 \\ 5(8)+3y=58 \\ 40+3y=58 \\ 3y=58-40 \\ 3y=18 \\ y=(18)/(3) \\ y=6 \end{gathered}`

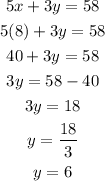
Solution: x=8 y =6

Then, A pound of jelly beans costs $8.00 and a pound of gummy worms costs $6.00