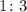Question

If rectangle ABCD is similar to rectangle LMNO as shown below, what is true about the ratio of the perimeter of rectangle ABCD to the perimeter of rectangle LMNO? 18 m N IC 3 m M (TDF.G.14.a)(1 point) O A. 1:9 O B. 3:1 O C. 1:2 O D. 1:3

Answer 1

The ratio of the perimeter of rectangle ABCD to the perimeter of rectangle LMNO is;

`1\colon3`

Step-by-step explanation:

Given the rectangles ABCD and LMNO are Similar;

The ratio of the sides of a similar rectangle is the same as the ratio of their perimeter;

`(l_(ABCD))/(l_(LMNO))=(P_(ABCD))/(P_(LMNO))`

The length of corresponding sides CD and NO are;

`\begin{gathered} CD=6m \\ NO=18m \end{gathered}`

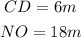
So, the ratio of the corresponding sides is;

`\begin{gathered} CD\colon NO \\ 6\colon18 \\ To\text{ the least form, dividing both sides by 6;} \\ 1\colon3 \end{gathered}`

And since the ratio for the sides and the perimeter are the same, then the ratio of the perimeter of rectangle ABCD to the perimeter of rectangle LMNO is;

`1\colon3`