Question

"the guidelines of the section" this means to graph and then state where the inflection points, critical points, absolute extremes, local extremes, asymptotes concave up and down points, etc#20

Answer 1

Given: A function

`f(x)=x^4+4x^3`

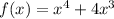
Required: To determine the critical points, inflexion points, local maxima, local minima, asymptotes and concavity of the function.

Explanation: To determine the critical points we put f'(x)=0.

Hence differentiating the function with respect to x gives-

`\begin{gathered} f^(\prime)(x)=4x^3+12x^2 \\ =4x^2(x+3) \end{gathered}`

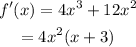
Putting f'(x)=0 gives

`\begin{gathered} 4x^2(x+3)=0 \\ \Rightarrow x=0\text{ or }x=-3 \end{gathered}`

Hence at x=0 and x=-3

`\begin{gathered} f(0)=0 \\ f(-3)=81-108 \\ =-27 \end{gathered}`

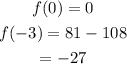
Hence the critical points are (0,0) and (-3,-27).

Now, for inflexion points we put f''(x)=0.

Hence differentiating f'(x) again gives-

`\begin{gathered} f^(\prime)^(\prime)(x)=12x^2+24x \\ =12x(x+2) \end{gathered}`

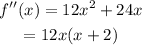
Putting f''(x)=0 gives

`x=0\text{ or }x=-2`

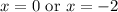
Hence the inflexion points are (0,0) and (-2,-16).

Checking the value of f''(x) at critical points-

`\begin{gathered} f^(\prime)^(\prime)(0)=0\text{ and} \\ f^(\prime)^(\prime)(-3)=36 \end{gathered}`

Hence the local minima is at x=-3.

There are no asymptotes as the given function is not rational.

Now to check for concavity we use the inflexion points to set up the intervals and check the value of f"(x) in the interval.

The concavity in the intervals are

`\begin{gathered} (-\infty,-2)\rightarrow f^(\prime)^(\prime)(x)\text{ is positive}\Rightarrow\text{ Concave UP} \\ (-2,0)\rightarrow f^(\prime)^(\prime)(x)\text{ is negative}\Rightarrow\text{ Concave Down} \\ (0,\infty)\rightarrow f^(\prime)^(\prime)(x)\text{ is positive}\Rightarrow\text{ Concave UP} \end{gathered}`

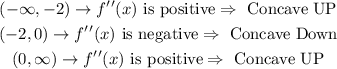
Now we can draw the graph of the function-

Final Answer: The graph of the function is drawn.