To determine if the lines of the equation system are parallel, perpendicular, equal, or not perpendicular, the first step is to write both equations in the slope-intercept form:
Equation 1
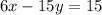
To write this equation in slope-intercept form, the first step is to pass the x-term 6x to the right side of the equation. For this, apply the opposite operation to both sides of it:
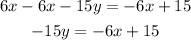
The next step is to divide both sides by -15:
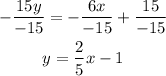
Equation 2:
This equation is already written on the slope-intercept form:
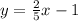
As you can see both equations are equal, this means that this equation system has infinite solutions.