Consider the general quadratic equation:

The discriminant of this equation is defined as:
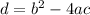
(a) Calculate the discriminant. Before we can use the formula, we need to transform the equation into the required form.
We are given:
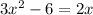
Subtracting 2x and rearranging:
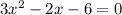
We can now identify the coefficients: a = 3, b = -2, c = -6, and compute the discriminant as follows:

(b) The discriminant gives important information about the solutions of the equation:
* If d is zero, there is only one real solution.
* If d is positive, there are two real solutions.
* If d is negative, there are two complex solutions.
In our equation, d is positive and the equation has two real solutions