The given equation is
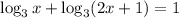
Use the rule
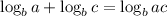
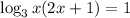
Change it to the exponent using the rule
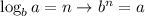
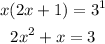
Subtract 3 from both sides
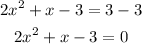
Factorize it
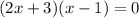
Equate each bracket by 0 to find x

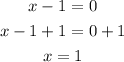
We will refuse x = -1.5 because we can not use negative numbersThank
with log
The answer is x = 1 only
The answer is D