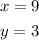Answer:
The number of bass caught is 9, while the number of trout caught is 3;
Step-by-step explanation:
Given that each bass weighed 3 pounds, and each trout weighed 1 pound.
Let x represent the number of bass and y represent the number of trout.
If Chloe caught a total of 30 pounds of fish, we have;
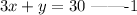
Also, She received 5 points in the competition for each bass, but since trout are low in Lake Poinsett, she lost 1 point for each trout.
If Chloe scored a total of 42 points, we have;
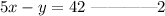
To solve;
Adding equations 1 and 2 together;
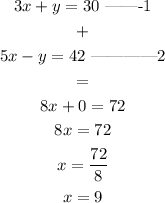
Solving for y;
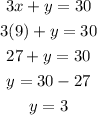
Therefore, the number of bass caught is 9, while the number of trout caught is 3;