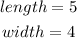Question

The length of a rectangle is 1 inches more than the width. The area is 20 square inches. Find the dimensions.The length of the rectangle is ?inches, while the width is ? inches.

Answer 1

Given:

There are given that the length of a rectangle is 1 inch more than the width.

Step-by-step explanation:

Suppose the value of width is x.

Then,

According to the question, the length of a rectangle is 1 inch more than the width:

So,

The value of width is;

`x+1`

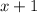
Now,

From the formula of area of a rectangle:

`\begin{gathered} A=length* width \\ 20=(x+1)* x \\ 20=x^2+x \\ x^2+x-20=0 \end{gathered}`

Then,

`\begin{gathered} x^(2)+x-20=0 \\ (x-4)(x+5)=0 \\ x=4,-5 \end{gathered}`

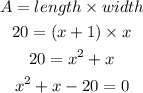
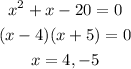
Then,

Put the value of x, i.e., 4, into the length and width.

So,

`\begin{gathered} width=x=4 \\ length=x+1=4+1=5 \end{gathered}`

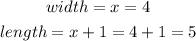
Final answer:

Hence, the dimension of the rectangle is shown below:

`\begin{gathered} length=5 \\ width=4 \end{gathered}`