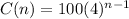Question

Every day, there are 4 times more likes on an internet video of a horse that is modeled by the function c(n) = (4)n − 1, where n is the number of days since the video posted. On the first day, there were 100 likes. What is the function that shows the number of likes each day? (1 point)c(n) = 100(4)n − 1c(n) = (4)(100)(n − 1)c(n) = (100)n − 1c(n) = (4)100 − 1

Answer 1

Given: The function below

`c(n)=(4)n-1`

To Determine: The functions that shows the number of likes each

Solution:

There were 100 likes the first day

`C(1)=100`

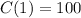
The given modelled function can be re-written as

`\begin{gathered} c(n)=C(1)*4^(n-1) \\ C(1)=100*4^(1-1) \\ C(1)=100*4^0 \\ C(1)=100*1 \\ C(1)=100 \end{gathered}`

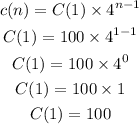
The above function defined the given number of likes for the first day.

Therefore, the number of likes for the second day would be

`\begin{gathered} C(2)=100*4^(2-1) \\ C(2)=100*4^1 \\ C(2)=100*4 \\ C(2)=400 \end{gathered}`

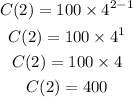
Hence, we can conclude that the function that shows the number of likes each day is

`C(n)=100(4)^(n-1)`