Answer:
Choice D. 2 solutions
Step-by-step explanation:
Adding the two equations gives
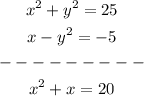
Therefore, we have the quadratic equations
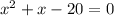
which has the solutions ( using quadratic formula)
![x=\frac{-1\pm\sqrt[]{1^2-4(1)(-20)}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/awekgkohrsotkgjcf66nptu73mfhup7e2g.png)
![x=\frac{-1\pm\sqrt[]{81}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/74hkf5mo2hilwzl7ywzpww63xwl2hw1r2f.png)
meaning we have two values of x that satisfy the system of equations.
Therefore, choice D is the correct answer.