Identify whether the equation represents an exponential growth or exponential decay function.1. y = 1/4 (1/e)^-2x2. y = (1/e)^4x3. y = 2e^-x + 1How do you do this?

Question

asked Jun 25, 2023 15.2k views

1 Answer

Gingo · Answer 1 · 2023-07-01T21:53:43+0000

The general formula for exponential growth and decays is:

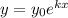
if k>0 then then it is an exponential growth function. If k<0 then the function represents an exponential decay.

Now we need to classify each of the functions:

1.

The function

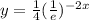
can be wrtten as:

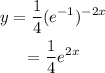
$\begin{gathered} y=(1)/(4)(e^(-1))^(-2x)^{} \\ =(1)/(4)e^(2x) \end{gathered}$

comparing with the general formula we notice that k=2, therefore this is an exponential growth.

2.

The function

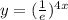
can be written as:

$\begin{gathered} y=((1)/(e))^(4x) \\ y=(e^(-1))^(4x) \\ y=e^(-4x) \end{gathered}$

comparing with the general formula we notice that k=-4, therefore this is an exponential decay.

3.

The function

comparing with the general formula we notice that k=-1, therefore this is an exponential decay.