Question

A parabola goes through three points (0, 8), (2, -6) and (-1,18). Find the equation of the parabola.

Answer 1

The parabola psses through the three points

`(0,8),(2,-6)\text{ and (-1,18)}`

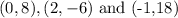
Using the form

`y=ax^2+bx\text{ +c}`

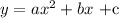
Substitute each of the point in for x and y into the form given above

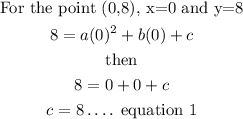
`\begin{gathered} \text{For the point (0,8), x=0 and y=8} \\ 8=a(0)^2+b(0)+c \\ \text{then} \\ 8=0+0+c \\ c=8\ldots\text{. equation 1} \end{gathered}`

then

`\begin{gathered} \text{For the point (2,-6) x=2,y=-6} \\ -6=a(2)^2+b(2)+c \\ -6=4a+2b+c\ldots\text{equation 2} \end{gathered}`

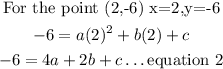
Similarly, for the last point, we have

`\begin{gathered} (-1,18),\text{then x=-1,y=18} \\ 18=a(-1)^2+b(-1)+c \\ 18=a-b+c\ldots\text{equation 3} \end{gathered}`

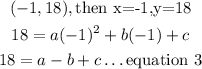
Substitute the equation1 into equation 2 and equation 3

`\begin{gathered} c=8\text{ into equation 2} \\ -6=4a+2b+8 \\ -6-8=4a+2b \\ -14=4a+2b \\ \text{Divide through by 2} \\ -7=2a+b \\ \text{Hence} \\ 2a+b=-7\ldots\text{ equation 4} \end{gathered}`

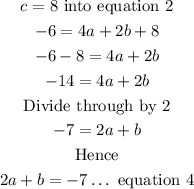
Similarly for equation 3, we have

`\begin{gathered} 18=a-b+c \\ \text{where c=8} \\ 18=a-b+8 \\ 18-8=a-b \\ 10=a-b \\ \text{Hence } \\ a-b=10\ldots\text{. equation 5} \end{gathered}`

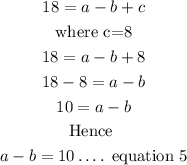
Hnece, solve equation 4 and 5 simultaneously for find the value of a and b

`\begin{gathered} 2a+b=-7 \\ a-b=10 \\ \text{ By elimination method, add the two equation above } \\ 3a+0=3 \\ 3a=3 \\ \text{divide both sides by 3} \\ a=(3)/(3)=1 \end{gathered}`

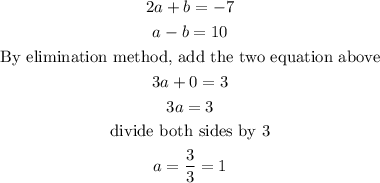
The substitute a=1 into equation 5 to obtain b

`\begin{gathered} a-b=10 \\ 1-b=10 \\ -b=10-1 \\ -b=9 \\ \text{Hence } \\ b=-9 \end{gathered}`

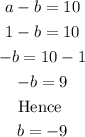
Hnece

`a=1,b=-9,c=8`

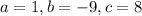
Substitute the values in the form below

`\begin{gathered} y=ax^2+bx+c \\ y=1x^2+(-9)x+8 \\ y=x^2-9x+8 \end{gathered}`

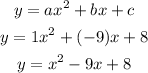
Then

`f(x)=1x^2+(-9)x+8`

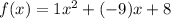
Therefore, the equation of the parabola is f(x)=1x²-9x+8

Answer: f(x)=1x²-9x+8