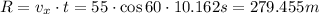Solution
For this case we can create the following plot:
We can use the following formula to find the time to reach the ground:
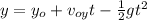
And we can assume that yo =0 and g= 9.8m/s^2 then we have this:
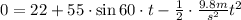
And solving we have this quadratic expression:
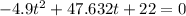
And then solving for t using the quadratic formula we got:
![t=\frac{-47.632\pm\sqrt[]{(47.632)^2-4\cdot(-4.9)\cdot(22)}}{2\cdot(-4.9)}](https://img.qammunity.org/2023/formulas/mathematics/college/6r6cfzmt54fw8uu8ofqyz5f9sugfakkihf.png)
Solving we got:
t= 10.162 s
And then we can find the horixontal distance with this formula: