Question

A woman invests a total of $20,000 in two accounts, one paying 4% and the other paying 9.5% simple interest per year. Her annual interest is $1,130. How much did she invest at each rate?

Answer 1

The simple interest per year is given by the following formula:

`A=p(1+rt)`

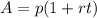
Where:

P= initial amount

r= rate

t= time

`A=p+prt`

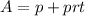
Where: prt is the annual interest.

Therefore:

`\begin{gathered} Interest4=prt=p_1*(0.04)(1) \\ Interest9=prt=p_2*(0.09)(1) \end{gathered}`

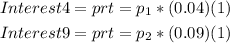
We know that:

`Interest4+Interest9=p_1(0.04)+p_2(0.09)`

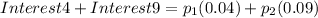
Also:

`Interest4+Interest9=1,130`

Replacing:

`1,130=p_1(0.04)+p_2(0,095)\text{ \lparen1\rparen}`

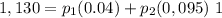
Secondly:

`p_1+p_2=20,000\text{ \lparen2\rparen}`

Isolating P1 in (2):

`p_1=20,000-p_2\text{ \lparen3\rparen}`

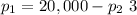
Substituing (3) in (1):

`\begin{gathered} 1,130=(20,000-p_2)*(0.04)+p_2(0.095) \\ 1,130=800-0.04p_2+0.095p_2 \\ 1,130-800=0.055p_2 \\ 0.055p_2=330 \\ p_2=(330)/(0.055)=6,000 \end{gathered}`

Finally, puttin P2=6,000 in equation (3):

`\begin{gathered} p_1=20,000-p_2 \\ p_1=20,000-6,000=14,000 \end{gathered}`

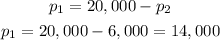
Answer: The amount she invest at each rate is $14,00 at 4% and $6,000 at 9.5%.