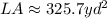Question

Find the lateral area of a right cylinder with a diameter of 6.4 yards and a height of 16.2 yards. Round to the nearest tenth.

Answer 1

You can use the following formula in order to calculate the Lateral area of the right cylinder given in the exercise:

`LA=2\pi rh`

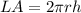
Where "LA" is the lateral area of the cylinder, "r" is the radius and "h" is the height.

In this case you know that its diameter is:

`d=6.4yd`

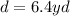
Since the diameter of a circle is twice the radius:

`2r=6.4yd`

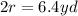
Knowing that the height of the cylinder is:

`h=16.2yd`

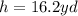
You can substitute values into the formula and then evaluate, in order to find the lateral area:

`\begin{gathered} LA=\pi(6.4yd)(16.2yd) \\ LA\approx325.7yd^2 \end{gathered}`

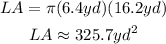
Then, the answer is:

`LA\approx325.7yd^2`