Given:
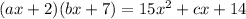
And
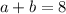
Required:
To find the two possible values of c.
Step-by-step explanation:
Consider
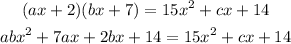
So
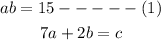
And also given
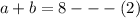
Now from (1) and (2), we get
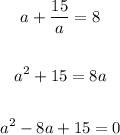
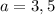
Now put a in (1) we get
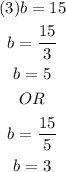
We can interpret that either of a or b are equal to 3 or 5.
When a=3 and b=5, we have
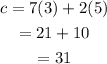
When a=5 and b=3, we have

Final Answer:
The option D is correct.
31 and 41