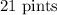Answer:
The amount of pint of the first drink type is;
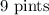
The amount of pint of the second drink type is;
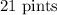
Step-by-step explanation:
Let x represent the amount of pint of the first type
The amount of the second type will be;

Since the total amount of the mixture is 30 pint.
Equating the amount of pure fruit in each type to that of the mixture.
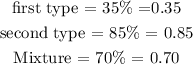
We have;
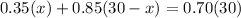
solving for x;
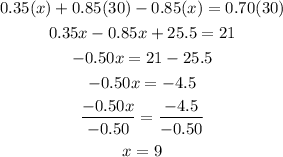
The amount of pint of the first type is;
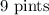
So, the amount of pint of the second type will be;
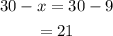
The amount of pint of the second type is;