For the car to stay on the road without sliding in or sliding out, all the forces on the x-axis must equal each other. Thus by equating all the forces on the x-axis, we can find the coefficient of the friction.
In order to determine the minimum speed of the car, use the following expression:
![v=\sqrt[]{R\cdot g\cdot\tan \theta}](https://img.qammunity.org/2023/formulas/physics/college/6gqglgkujkj0h20uj1y67jyhwhzpr9sa9h.png)
where,
R: radius of the road = 84m
g: gravtitational acceleration constant = 9.8m/s^2
θ: angle of banking of the road = 17 degrees
Replace the previous values of the parameters into the formula for v:
![\begin{gathered} v=\sqrt[]{(84m)(9.8(m)/(s^2))(\tan 17)} \\ v\approx15.86(m)/(s) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/mfdft1ggwfvmy1i9cxxt3mf7v3lwhnkvtg.png)
Hence, the minimum speed requierd is approximately 15.86m/s
In order to determine the value of the minimum coefficient friction required, use the following formula:
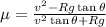
by replacing, you get:
![undefined]()