To find the rate of change
Simply calculate the slope of the line
From the graph the two points are given
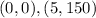
The slope of the line can be calculated using

Where m is the slope of the line
From the given points
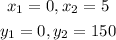
Substitute the values into the equation
This gives
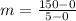
Simplify further
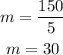
Since the slope og the line is 30
This implies that the rate of change is $30