Statement Problem: Let;
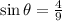
Find the exact value of;
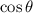
Solution:
In trigonometry, the ratio of the sine is defined as;
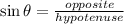
Thus,

By Pythagoras theorem, the square of the longest side (hypotenuse) is the sum of squares of the opposite and the adjacent sides.
![\begin{gathered} (\text{hypotenuse)}^2=(\text{opposite)}^2+(\text{adjacent)}^2 \\ (\text{adjacent)}^2=(\text{hypotenuse)}^2-(\text{opposite)}^2 \\ (\text{adjacent)}^2=9^2-4^2 \\ (\text{adjacent)}^2=81-16 \\ (\text{adjacent)}^2=65 \\ \text{adjacent}=\sqrt[]{65} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vuwwd3ywih7dluje9k9wupsjfsp4axfzoo.png)
The ratio of the cosine is defined as;
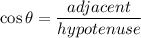
Hence,
![\cos \theta=\frac{\sqrt[]{65}}{9}](https://img.qammunity.org/2023/formulas/mathematics/college/tueiia4vgmg9bo5dr9i62ydid6nwwbqe49.png)