Question

I am trying to find the value of x, y, and z.

Answer 1

`\begin{gathered} x=\sqrt[]{35}=5.62 \\ y=\sqrt[]{60}=7.75 \\ z=\sqrt[]{84}=9.17 \end{gathered}`

Step-by-step explanation: We need to find x y z, three missing sides:

From the given triangle, we can form three equations, using the Pythagorean theorem as:

`\begin{gathered} (1)\rightarrow5^2+x^2=y^2 \\ (2)\rightarrow7^2+x^2=z^2 \\ (3)\rightarrow z^2+y^2=(7+5)^2=12^2 \\ \end{gathered}`

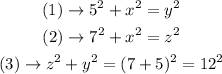
Solution by substitution:

Substituting (1) in (3) gives:

`\begin{gathered} z^2+5^2+x^2=12^2 \\ z^2+25+x^2=144 \\ z^2+x^2=144-25=119 \\ z^2+x^2=119\rightarrow(4) \end{gathered}`

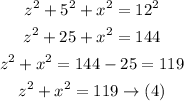
We have reached equation (4), solving for z in equation (4), and then substituting it into equation (2) gives:

`\begin{gathered} 7^2+x^2=119-x^2\rightarrow2x^2=119-49=70 \\ \therefore\rightarrow \\ x=\sqrt[]{(70)/(2)}=\sqrt[]{35}=5.916 \end{gathered}`

Plugging this x into equation (4) gives:

`\begin{gathered} z^2+(\sqrt[]{35})^2=119\rightarrow z^2=119-35=84 \\ \therefore\rightarrow \\ z=\sqrt[]{84}=9.165 \\ \\ \end{gathered}`

Now that we have x and z, we plug x it into equation (1) and we get:

`\begin{gathered} 5^2+(\sqrt[]{35})^2=y^2 \\ \therefore\rightarrow \\ y^2=25+35=60 \\ y=\sqrt[]{60}=7.75 \end{gathered}`

x y z respectively are:

`\begin{gathered} x=\sqrt[]{35}=5.62 \\ y=\sqrt[]{60}=7.75 \\ z=\sqrt[]{84}=9.17 \end{gathered}`