In order to find a simplified expression for the area of the rectangle, we just need to multiply the expressions of the length and width. So we have that:
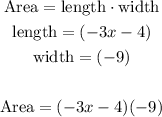
Then, using the distributive property, we can expand the product:
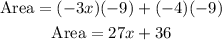
So the simplified expression for the area is 27x + 36