An equation with no solutions, is whne no matter what the unknown is, it never will be true.
First, we can have the same unknown on both sides: 3x
And then we can solve the left hand side of the equation, adding all the numbers:
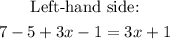
Now, if we have the same 3x in the right:
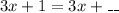
We have to add in the right side of the equation a number different from 1. Let's take 2. Then we have:
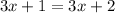
And we can verify that this equation does not have any solutions, by substracting 3x on both sides, and we get:

Which is never true, and thus the euqation does not have any solutions.