Question

A spinner is mounted on a piece of cardboard divided into six areas of equal size. Each of the six areas is a different color (blue, yellow, red, green, white, and orange). When the spinner is spun, each color should be selected by the spinner approximately ⅙ of the time. A student suspects that a certain spinner is defective. The suspected spinner is spun 90 times. The results are shown below. Test the students claim. Use a=0.10 Color: Blue, Yellow, Red, Green, White, OrangeFrequency: 12, 11, 17, 16, 19, 15

Answer 1

Let's write the given results:

Color Frequency

Blue 12

Yellow 11

Red 17

Green 16

White 19

Orange 15

The expected frequency of each color must be,

`Expected\text{ Frequency = }\frac{90\text{ turns}}{6}`
`\text{Expected Frequency = 15}`

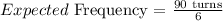
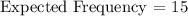
Thus,

Color Frequency Expected (Recored - Expected)^2/Expected

Blue 12 15 0.60

Yellow 11 15 1.07

Red 17 15 0.27

Green 16 15 0.07

White 19 15 1.07

Orange 15 15 0.00

Chi-Square (χ2)= 3.08

Degree of freedom = 6 - 1 = 5.

Alpha level (α) = 0.10

Thus, it will give you a p-value of 0.6897.

Since 0.6897 > 0.10, we fail to reject the null.

Conclusion: There is no sufficient evidence to support the student's claim that the spinner is defective.