Given:
center (h, k) at (-10, -4)
point on the center at (4, -2).
Find: equation of the circle in standard form

where (h, k) is the coordinate of the center and r = length of the radius.
Solution:
Since the coordinate of the center has been provided already, let's just calculate the radius. The radius is the center from the center to any point on the circle. To get the distance, let's use the distance formula between two points.

Let's plug into the formula above the coordinate of the two points. The first point is the center while the point on the circle is our second point.
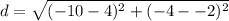
Then, solve.
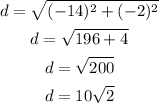
Hence, our radius is 10√2 units.
Let's now plug into the equation in standard form of a circle its radius and the coordinate of its center.

Answer:
The equation is (x + 10)² +(y + 4)² = 200.²