Given the series
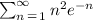
The n-th term of the series is
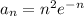
Use the ratio test to check the convergence.
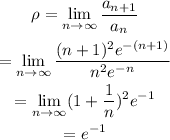
If the limit is less than 1, the series converges. If the limit is greater than 1, then the series diverges and if it equals 1, then the test fails.
Here the value of the limit is < 1, since e > 1. So, the given series converges.