Consider the angle formed by the lines RS and RT. This is the angle that we want find. In general, for a circle, the arc formed by two lines that start at the center of the circle has a lenght that is related to the angle (in radians) formed by the lines and the radius of the circle by the following formula.
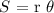
where S is the arc lenght. In our case, we have
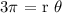
In this case, r is the radius of the circle, which is known to be the lenght of the line RS, which is 12.
So, we get the equation
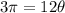
If we divide on both sides by 12, we get

so the angle is pi/4.. By using an approximation for the value of pi (3.1416) so you can find a value of theta of 0.785 radians, which rounded to the neares hundredth is 0.79 radians