Question

Can you please solve this as if you didn’t have a calculator (also I began working on it got lost and quit)

Answer 1

To find the x-intercept, we need to find the zeros of the function:

`f(x)=0`

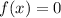
We can do that by factoring the function. We start by factoring out the -x:

`\begin{gathered} f(x)=-x^3+6x^2-9x \\ f(x)=-x(x^2-6x+9) \end{gathered}`

Now, we can see that the quadratic factor left is in the form of the square identity:

`\begin{gathered} (x-a)^2=x^2-2ax+a^2 \\ a=3\colon \\ (x-3)^2=x^2-6x+9 \end{gathered}`

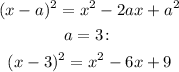
So, the factored function is:

`f(x)=-x(x-3)^2`

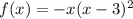
This means that the zeros of the function are:

`\begin{gathered} x=0 \\ x-3=0\Longrightarrow x=3 \end{gathered}`

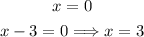
Also, since the factor of the zero x = 3 is squared, it has multiplicity of 2, and since the factor of the zero x = 0 is simply x, it has multiplicity of 1.

So, the zeros are:

x = 0, point (0, 0), multiplicity 1

x = 3, point (3, 0), multiplicity 2

Which means that the x-intercepts are x = 0, where the functions passes right through, and x = 3, where the function only touches the x-axis.

The y-intercept is where x = 0:

`f(0)=-0(0-3)^2=-0\cdot9=0`

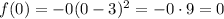
So, the y-intercept is at y = 0, point (0, 0).

Since it is a polynomial, the end behaviors are to infinity, and since it is a 3rd degree polynomial one endbehavior is the opposite infinity of the other.

When the leading coefficient is positive, the end behaviors of an odd degree polynomial are minus infinity on the left and plus infinity on the right.

When the leading coefficient is negative, this will be switched, so the end behavior of the left is plus infinity and the end behavior os the right is minus infinity.

In this case, the leading coefficient is negative, so the left end behavior is upwards and the right end behavior is downwards, that is:

`\begin{gathered} as\; x\to-\infty,f(x)\to+\infty \\ as\; x\to+\infty,f(x)\to-\infty \end{gathered}`

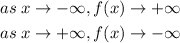
Or, in limit notation:

`\begin{gathered} \lim _(x\to-\infty)f(x)=+\infty \\ \lim _(x\to+\infty)f(x)=-\infty \end{gathered}`

So, from left to right, the function come from positive values until it crosses the x-axis and y-axis at the same point, (0, 0). It goes down for a while and then it reaches a minimum and starts going up again until it touches the x-axis at x = 3, making a maximum there and then going dowards again.

We will have the following graph: