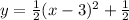Question

Write the formula for a quadratic function with the indicated characteristics. Has vertical intercept at Q = 5 and a minimum value at the point (3, 1/2)

Answer 1

`y=(1)/(2)(x-3)^2+(1)/(2)`

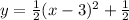
Step-by-step explanation:

The vertex form of a quadratic equation is generally given as;

`y=a(x-h)^2+k`

where (h, k) represents the coordinate of the vertex of the parabola.

Given a vertical intercept of 5, this means that x = 0 at y = 5. We're also given that the function has a minimum value at the point (3, 1/2), this means that h = 3 and k = 1/2.

Let's go ahead and substitute the above values into the vertex equation and solve for a;

`\begin{gathered} 5=a(0-3)^2+(1)/(2) \\ 5=9a+(1)/(2) \end{gathered}`

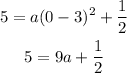
Let's subtract 1/2 from both sides of the equation;

`\begin{gathered} 5-(1)/(2)=9a \\ (10-1)/(2)=9a \\ (9)/(2)=9a \end{gathered}`

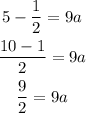
Let's now divide both sides by 9;

`\begin{gathered} (9a)/(9)=((9)/(2))/(9) \\ a=(9)/(2)\cdot(1)/(9) \\ a=(1)/(2) \end{gathered}`

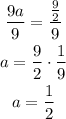
Since a = 1/2, h = 3, and k = 1/2, we can go ahead and write the required formula in vertex form as;

`y=(1)/(2)(x-3)^2+(1)/(2)`