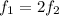Question

An air column open at both ends is 1.00 m long. If the speed of sound is 340 m/s and resonance occurs, what are the two lowest resonant frequencies, and what relationship exists between these two notes?

Answer 1

We are asked to determine the frequency of an open air column. To do that we will use the following formula:

`f_1=(V)/(2L)`

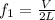
Where:

`\begin{gathered} V=\text{ sp}eed\text{ of sound} \\ L=\text{ length} \\ f_1=\text{ frequency} \end{gathered}`

Substituting the values:

`f_1=(340(m)/(s))/(2(1m))`

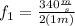
Solving the operations we get:

`f_1=170Hz`

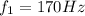
Therefore, the first frequency is 170 Hz.

To determine the second frequency we use the following formula:

`f_2=(V)/(L)`

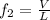
Substituting the values we get:

`f_2=(340(m)/(s^2))/(1m)`

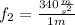
Solving the operation we get:

`f_2=340Hz`

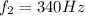
Therefore, the second frequency is 340 Hz.

We notice that the relationship between frequency is:

`f_1=2f_2`