Question

Blue points, blue line segments, red points, and red line segments arranged on a Cartesian coordinate plane. Here are the blue points and their coordinates. Point A: (negative nine, 3). Point B: (negative 11, 3). Point C: (negative 10, 3). Point D: (negative 10, 5). Point F: (negative 10, 4). Point E: (negative 11, 4). Here are the red points and their coordinates. Point A-1: (negative 1, 6). Point A-2: (negative 3, 4). Point B-1: (negative 2, 4). Point B-2: (negative 5, 4). Point C-2: (negative 3, 3). Point D-1: (negative 5, 5). Point D-2: (negative 5, 3). Point E-1: (negative 6, 6). Point F-1: (negative 5, 6). A semicircle that lies below its line of symmetry AB. A semicircle that lies above its line of symmetry B-2 A-2. A triangle DEF. A triangle D-1 E-1 F-1. Line segments are drawn from C to D, from A-1 to B-1, from A-2 to B-2, and from C-2 to D-2. Triangle DEF, segment CD, and the semicircle with line of symmetry BA are arranged so that they look like a boat.1.What transformations would you use on the blue triangle to get it to match with the red triangle? Explain your movement using the coordinates of the vertices.

Answer 1

Transformation blue triangle.

Point D.

coordinates(-10,5)

and the point D1 have coordinates: (-5,5)

The transformation will be over the x-axis:

`\begin{gathered} D(-10,5) \\ D(-10+5,5)=(-5,5) \end{gathered}`

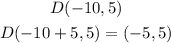
Point F.

Coordinates(-10,4 ).

Ans the point F1 have coordinates: ( -5,6)

The transformation will be over both axis, x and y:

`\begin{gathered} F=(-10,4) \\ F(-10+5,\text{ 4+2 })=(-5,\text{ 6}) \end{gathered}`

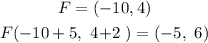
Point E.

Coordinates: (-11,4)

The point E1 have coordinates: (-6, 6),

The tranformation will be over both axis once again.

`\begin{gathered} E(-11,\text{ 4}) \\ E(-11+5,\text{ 4+2})=(-6,6) \end{gathered}`

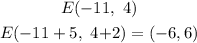
Conclusion: on the x-axis, it shifts 5 points to the right, while on the y-axis it shifts up 2 points only for points E and F.