Question

Meghantrainer spent 180 to start a dog-walking business and earns $8 for each dog she walks Nicki Minaj doesn't spend anything to start a business and already has $160 saved up Nicki Minaj and $6 for every dog she walks how many dogs would they each have to walk before they have the same amount of money

Answer 1

We will investigate the accounts of two people ( Meghan Trainer and Nicky Minaj ) for a particular business.

We will first develop accout statement for Meghan Trainer. She spent a certain amount of money to start her business i.e she started with a loss! We will go ahead and record this on her account statement as follows:

`\text{Account ( Meghan Trainer ) = -\$180}`

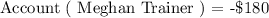
We will go ahead and define a variable for the number of dogs Meghan Trainer walks as follows:

`\text{\textcolor{#FF7968}{Number of dogs walked by Meghan Trainer = x}}`

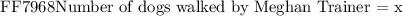
Now we are given that Meghan Trainer earns at a fixed rate per number of dogs walked. We will go ahead and determine the value of her account on an ( unknown number - x ) of dogs walked as follows:

`\begin{gathered} \text{Rate = }\frac{\text{\$}8}{\text{dog}} \\ \\ \text{Amount Earned ( Meghan Trainer ) = Rate}\cdot x \\ \text{\textcolor{#FF7968}{Amount Earned ( Meghan Trainer ) = \$8x}} \end{gathered}`

We will go ahead and update her acccount based on the amount she earned as follows:

`\text{\textcolor{#FF7968}{Account ( Meghan Trainer ) = -\$180 + \$8x}}`

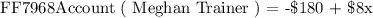
Now we will set up an account for Nicky Minaj. She has saved some amount initially for her business and did not spend any amount on starting the business. We will go ahead and record this amount in her account as follows:

`\text{Account ( Nicky Minaj ) = \$160}`

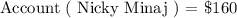
We will go ahead and define a variable for the number of dogs Nicky Minaj walks as follows:

`\text{\textcolor{#FF7968}{Number of dogs walked by Nicky Minaj = y}}`

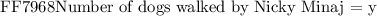
Now we are given that Nicky Minaj earns at a fixed rate per number of dogs walked. We will go ahead and determine the value of her account on an ( unknown number - y ) of dogs walked as follows:

`\begin{gathered} \text{Rate = }\frac{\text{\$}6}{\text{dog}} \\ \\ \text{Amount Earned ( }NickyMinaj\text{ ) = Rate}\cdot y \\ \text{\textcolor{#FF7968}{Amount Earned ( }}\textcolor{#FF7968}{NickyMinaj}\text{\textcolor{#FF7968}{ ) = \$6y}} \end{gathered}`

We will go ahead and update her acccount based on the amount she earned as follows:

`\text{\textcolor{#FF7968}{Account ( Nicky Minaj ) = \$160 + \$6y}}`

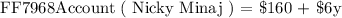
Now we have two accounts as follows:

`\begin{gathered} \text{Account ( Nicky Minaj ) = \$160 +\$6y} \\ \text{Account ( Meghan Trainer ) = -\$180 + 8x} \end{gathered}`

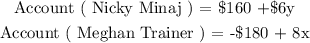
We are to determine the values of ( x and y ) such that the value of both accounts is the same. We will go ahead and equate both off the above accounts as follows:

`\begin{gathered} \text{Account ( Meghan Trainer ) = Account ( Nicky Minaj ) } \\ \text{\textcolor{#FF7968}{-\$180 + \$8x = \$160 +\$6y}} \end{gathered}`

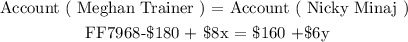
Now we will express either of the variables in terms of the other variable. We will express ( y ) in terms of ( x ) as follows:

`\begin{gathered} 6y\text{ = -340 + 8x} \\ \\ \textcolor{#FF7968}{y}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{\frac{8x\text{ - 340}}{6}} \\ \end{gathered}`

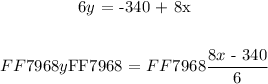
We see that the accounts to be equal or off same value the number dogs walked by Nicky Minaj ( y ) is a function of number of dogs walked by Meghan Trainer ( x ). We can go ahead and express the above relation graphically as follows: