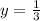Question

Identify the horizontal and vertical asymptotes of the graph of the rational function f(x) = (x^2 - 4)/(3x^2 + x - 4)

Answer 1

We are given the function

`f(x)=(x^2-4)/(3x^2+x-4)`

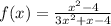
First, to get the Vertical asymptotes, we only need to equate the denominator to zero and then solve for x

`\begin{gathered} 3x^2+x-4=0 \\ \\ 3x^2-3x+4x-4=0 \\ \\ 3x(x-1)+4(x-1)=0 \\ \\ (x-1)(3x+4)=0 \\ \\ x=1,-(4)/(3) \end{gathered}`

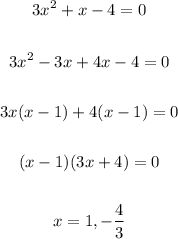
Therefore, the Vertical Asymptotes are

`\begin{gathered} x=1 \\ and \\ x=-(4)/(3) \end{gathered}`

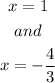
To get the horizontal asymptotes, we only need to take the highest power of x from both numerator and denominator

`\begin{gathered} y=(x^2)/(3x^2) \\ \\ y=(1)/(3) \end{gathered}`

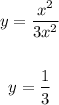
Therefore, the horizontal asymptotes is

`y=(1)/(3)`