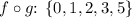In set notation:
- Domain of
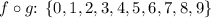
- Range of
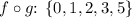
In the composition of two functions,
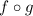 , we first apply
, we first apply
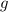 and then
and then
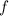 to the result. The domain of the composition will be the set of all inputs for
to the result. The domain of the composition will be the set of all inputs for
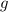 that map to outputs of
that map to outputs of
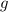 which are in the domain of
which are in the domain of
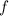 . The range of the composition will be the set of all possible outputs from
. The range of the composition will be the set of all possible outputs from
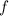 after
after
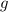 has been applied.
has been applied.
To find the domain of
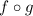 , we look at the domain of
, we look at the domain of
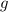 and see where those values map to in
and see where those values map to in
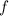 . The domain of
. The domain of
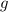 is the set of all x-values in its left oval, and the range is the set of all values it maps to in the right oval, which then must be in the domain of
is the set of all x-values in its left oval, and the range is the set of all values it maps to in the right oval, which then must be in the domain of
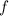 .
.
From the figure provided:
- The domain of
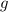 appears to be {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
appears to be {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
- The range of
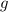 is {0, 1, 2, 3, 4, 5, 6} since these are the values
is {0, 1, 2, 3, 4, 5, 6} since these are the values
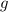 maps to.
maps to.
- The domain of
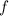 is {0, 1, 2, 3, 4, 5, 6}.
is {0, 1, 2, 3, 4, 5, 6}.
Since the range of
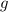 matches the domain of
matches the domain of
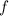 , the domain of
, the domain of
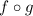 will be the same as the domain of
will be the same as the domain of
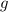 because all outputs from
because all outputs from
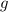 are valid inputs for
are valid inputs for
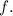
Therefore, the domain of
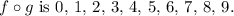
To find the range of
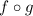 , we look at the range of
, we look at the range of
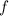 since it is the last function applied. However, we need to consider only the values of the range of
since it is the last function applied. However, we need to consider only the values of the range of
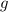 that are also in the domain of
that are also in the domain of
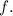
- The range of
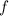 appears to be {0, 1, 2, 3, 5} since these are the values
appears to be {0, 1, 2, 3, 5} since these are the values
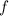 maps to from its domain.
maps to from its domain.
However, we have to map the values from the domain of
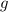 through
through
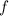 to get the range of
to get the range of
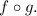
Mapping the domain of
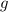 through
through
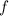 , we get the range of
, we get the range of
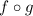 as the values that
as the values that
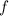 maps to, which appear to be {0, 1, 2, 3, 5}. Hence, the range of
maps to, which appear to be {0, 1, 2, 3, 5}. Hence, the range of
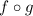 is {0, 1, 2, 3, 5}.
is {0, 1, 2, 3, 5}.
In set notation:
- Domain of
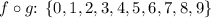
- Range of