the answer is 26 grams
Step-by-step explanation
We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:
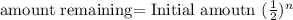
where n is the time
Step 1
Let
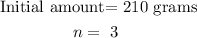
replace

so, the answer is 26 grams
i hope this helps you