Question

Runner A is initially 5.0 mi west of a flagpole and is running with a constant velocity of 5.0 mi/h due east. Runner B is initially 2.0 mi east of the flagpole and is running with a constant velocity of 4.0 mi/h due west. How far are the runners from the flagpole when they meet?_________ mi

Answer 1

1.11 miles

Step-by-step explanation

Step 1

Diagram

so

a)let

for runner A

`\begin{gathered} distance\text{ traveled by runner A=}x \\ velocity_A=5(mi)/(h) \\ time\text{ taken=t}_1 \end{gathered}`

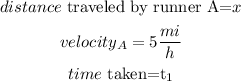
for runner B

`\begin{gathered} distance\text{ = y} \\ velocity_B=4\text{ }(mi)/(h) \\ time_2=time_1=(\text{ the same time taken when they meet\rparen} \end{gathered}`

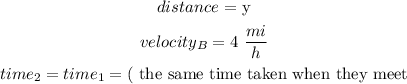
also we know that

`x+y=7\text{ }\Rightarrow equation\text{ \lparen1\rparen}`

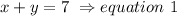
b) to set the equation, we need to apply the formula

`time=\text{ }\frac{distance\text{ }}{speed}`

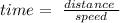
so

`\begin{gathered} time_1=time_2 \\ replace \\ (x)/(5(m)/(s))=(y)/(4(m)/(s)) \\ (x)/(5)=(y)/(4) \\ cross\text{ multiply} \\ 4x=5y \\ divide\text{ both sides by 4} \\ (4x)/(4)=(5y)/(4) \\ x=(5)/(4)y\Rightarrow equation\text{ \lparen2\rparen} \end{gathered}`

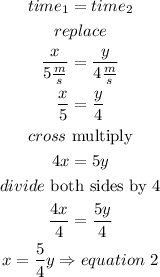
Step 2

solve the equations

replace the x value from equation (2) into equation(1) and solve for y

finally, replace in eq ( 1) to find the x value

so, they are

so,they are

1.11 miles far away from the flagpole