Answer:
• (a)80 mg
,
• (c)f(t)=80(0.5)^t
,
• (d)0.625 mg
Explanation:
Part A
From the point (0, 80), we see that the person took 80 mg of the medicine at the start.
Part B
From the graph:
From points (0,80) and (2,20); and (2,20) and (4,5)
• After 2 hours, the amount of medicine has been reduced by a factor of 1/4.
Therefore, after 1 hour, the amount of medicine is reduced by a factor of 1/2.
The completed table is attached below:
Part C
An exponential function is written in the form:
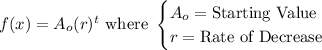
Since the amount of medicine is halved every 1 hour:
The rate of decrease = 1/2
The starting amount, Ao = 80 mg
Therefore, an equation that defines f is:
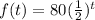
Part D
After 7 hours, when t=7
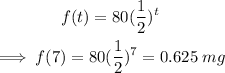
After 7 hours, 0.625 mg of medicine remains in the person's body.