Question

You are on top of a building 44.2 m tall. An adjacent building is 98.1 m tall. You throw a ball upward so that the ball lands on the roof of the adjacent building 4.15 s after it is thrown. What will be the speed of the ball when it lands on the roof of adjacent building?

Answer 1

Let's make a diagram to visualize the problem.

It's important to know that this motion is not like a parabola because the ball is thrown upwards. First, we find the initial velocity.

`h=v_0t+(1)/(2)gt^2`

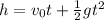
Using the given magnitudes, we have the following

`\begin{gathered} 53.9=v_0\cdot4.15+(1)/(2)\cdot(-9.8)\cdot(4.15)^2 \\ 53.9=4.15v_0-84.40 \\ 53.9+84.40=4.15v_0 \\ v_0=(138.3)/(4.15)((m)/(s)) \\ v_0\approx33.33((m)/(s)) \end{gathered}`

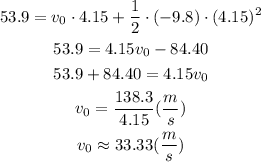
The initial velocity is 33.33 m/s.

Now we are able to find the final velocity of the ball.

`\begin{gathered} v_f=v_0+gt \\ v_f=33.33-9.8\cdot4.15 \\ v_f=33.33-40.67 \\ v_f=-7.34((m)/(s)) \end{gathered}`

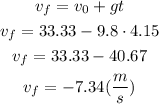
Therefore, the speed of the ball when it lands on the roof of the adjacent building is 7.43 m/s, going downwards.